Composition
Magmatic rocks possess variegated chemical, modal and mineralogical compositions, which depend on their origin. Proper genetic interpretation of magmatic rocks requires also knowledge on their texture and geotectonic setting. Apart from major and minor minerals, accessory minerals are also important for deciphering origin of magmatic rocks. Some accessory minerals are used for geochronology. Trace elements yield basis for construction of discrimination diagrams, which define geotectonic setting.
Mineral composition
Only a limited amount of minerals is known to crystallize directly from silicate magma, compared to overall number of known mineral species. Minerals of magmatic rocks can be subdivided into major (rock-forming), minor and accessory.
Major rock-forming minerals of magmatic rocks are as follows: olivine, pyroxene, amphibole, biotite, muscovite, plagioclase, alkalic feldspar, quartz and Fe-Ti oxides, mainly magnetite and ilmenite. These minerals comprise more than 10 wt. % of rock. Apart from quartz, all these minerals represent solid solutions, although quartz can also contain minute amounts of Al3+ and Li+ substituting for Si4+. Small amount of (OH)- can substitute for O2- in quartz structure. Apart from Fe-Ti oxides, all remaining rock-forming minerals are silicates, which crystallize consecutively from magma during a temperature decrease in accord with the Bowen’s reaction scheme (Fig. 2) named after Norman L. Bowen who proposed the scheme according to his own experiments with molten magmatic rocks of different compositions in 1920-1930. Carbonates belong to major rock-forming minerals in special magmatic rocks – carbonatites. Macroscopic study of magmatic rocks is important for identification of mineral assemblages, i.e. coexisting mineral associations.
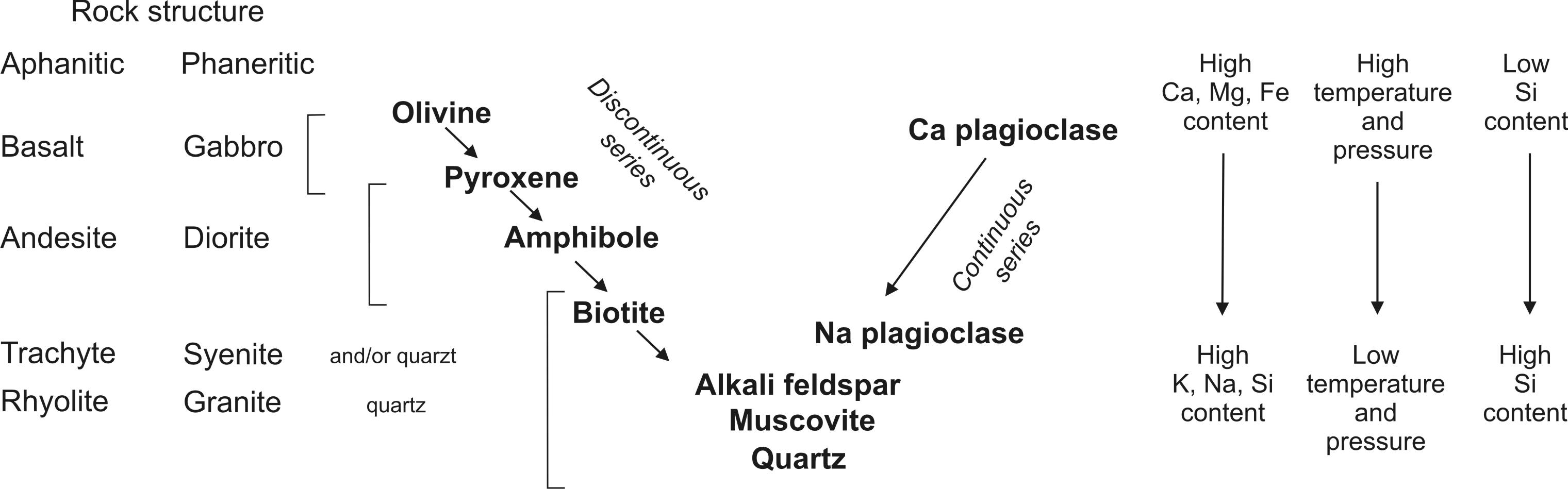
Fig. 2. Bowen’s reaction scheme, and its relationship to texture, chemical composition and formation P-T conditions.
Minerals occupying 3-10 wt. % of rocks are called minor. Minerals occupying less than 3 wt. % of rock are accessory. Despite low abundance, they contain high concentrations of actinides and high-field-strength elements, and can be thus used for age determination.
Some common and special accessory minerals are listed in Table 1. Some minerals that are accessory in certain rock-types can be major rock-forming minerals in others (e.g. apatite, zircon).
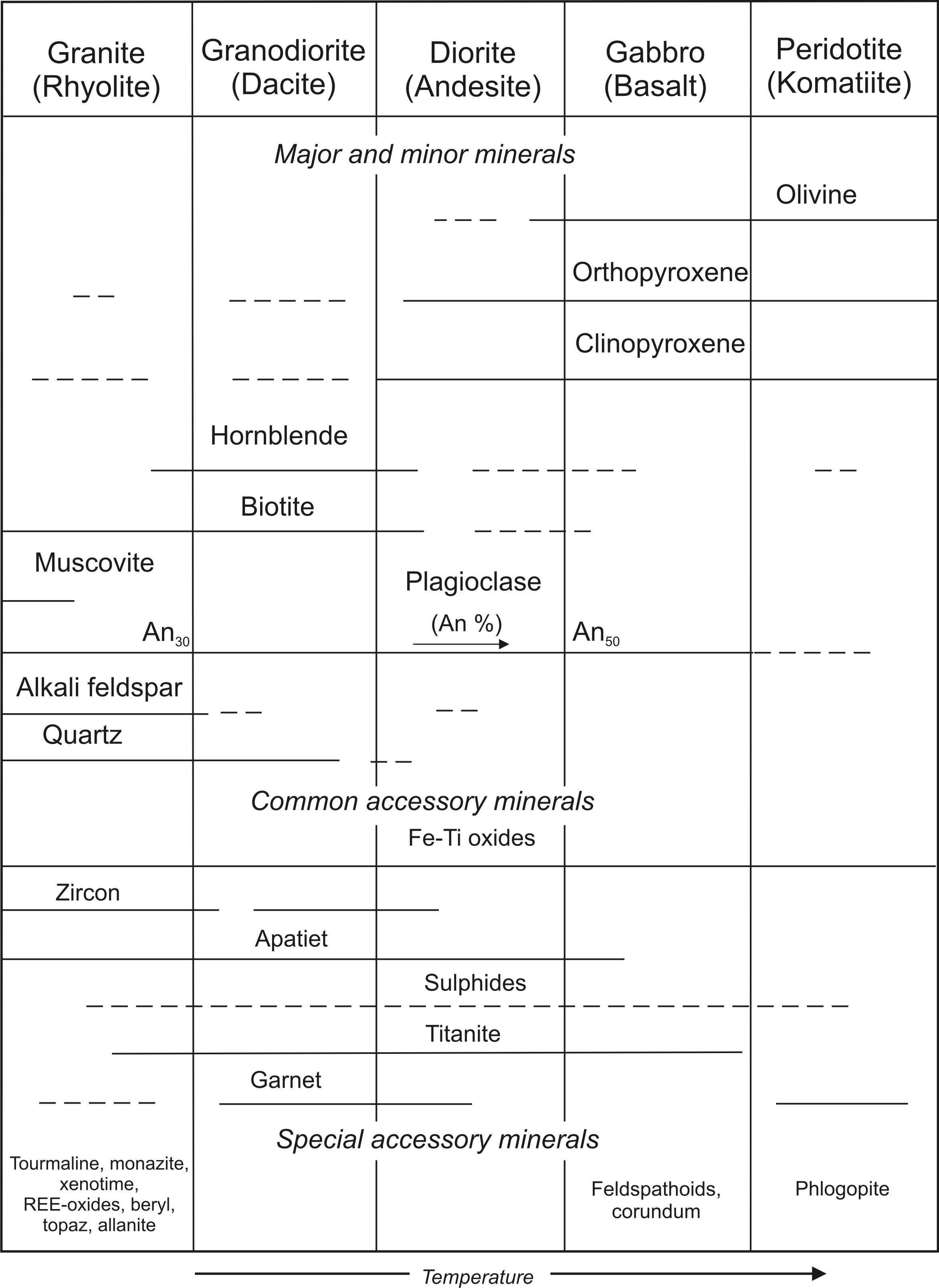
Table 1: The most frequent mineral assemblages of common sub-alkalic magmatic rocks. The first row contains phaneritic plutonic magmatic rocks and their aphanitic, volcanic equivalents (rhyolite, dacite, andesite, basalt, komatiite) are listed in parentheses. For instance, basalt (gabbro) contains plagioclase with the anorthite endmember content exceeding 50 molar percent (An>50), together with clinopyroxene, orthopyroxene, and olivine. Hornblend and biotite are present in minor amounts. Accessoric phases are represented by Fe-Ti oxides, apatite, titanite, some sulphides and corundum. Feldspathoids can be present as minor minerals. An increased Mg/Fe ratio in mafic minerals together with increased Ca/Na and K/Na ratios in plagioclases tends to reflect increased temperature (modified and completed after Best and Christiansen 2001).
Volcanic glass is important phase of magmatic rocks. Glass is not a mineral. It originates by rapid cooling of magma, sothat atoms and molecules do not have time to create well-organized crystallographic ordering typical of minerals. Instead of this, melt solidifies as highly viscous amorphous glass – super-undercooled solution of O, Si, Al, Ca and K with fragments of crystal structures in form of monomers, dimers, tetrahedral groups, etc. (Best and Christiansen 2001). Glass occurs in all types of volcanic rocks as well as along chilled margins of thin dykes emplaced close to surface.
According to glass content, the following types of volcanic rocks are distinguished:
- 1. rocks with glass (0-20 % of glass)
- 2. rocks rich in glass (20-50 % of glass)
- 3. glassy rocks (50-80 % of glass)
- 4. volcanic glass with more than 80 % of glass phase – obsidian, pemza, perlite, pitchstone
Chemical composition
More than 99 % of all magmatic rocks are composed of only 11 main molecules: SiO2, TiO2, Al2O3, Fe2O3, FeO, MnO, MgO, CaO, Na2O, K2O and P2O5. Iron occurs as divalent ferrous or trivalent ferric iron. If a given analytical method does not permit distinguishing between the iron oxidation states, total iron is expressed as either Fe2O3t or FeOt.
Element with a concentration in excess of 0.1 wt. % (>1000 ppm) is major element. In spite of the fact that analytical methods usually express concentrations as ppm (parts per million – one millionth – 1 gram per tonne) or ppb (parts per billion), concentration of major elements is expressed in weight percents of oxides, thus being in accord with the spirit of “wet” chemical analysis belonging to traditional methods of chemical composition determination.
Elements with concentrations less than 0.1 wt. % (<1000 ppm) are called trace elements. They are usually expressed in ppm or ppb units. Since the second half of 20th century, the classic “wet” chemical analysis has been complemented by modern methods, such as atomic absorption spectroscopy (AAS), flame photometry, mass spectrometry with inductively coupled plasma (ICP-MS), X-ray fluorescence analysis (XRF) and many others.
Many silicate rocks contain volatile components, such as water, carbon dioxide, sulphur, fluorine, or chlorine.
H2O+ is structurally bound water, or that bound as hydroxyl group in amphiboles, micas, iron oxides, clays, and molecular water in glass.
H2O- is wetness of rock, i.e. water in pores or that adsorbed on grain interfaces released by heating to 110 °C.
Significant CO2 in a magmatic rock, except for carbonates and alkalic rocks, occurs in secondary carbonates, originating during weathering or hydrothermal alteration.
The total content of volatiles – loss of ignition (LOI) is determined by comparison of equivalent amount of powdered sample prior and after heating to 1000 °C. Acceptable chemical analysis has a total of main oxides including H2O+ in the range of 98.8-100.8 wt. % (Best and Christiansen 2001).
Chemical composition of a rock can be expressed as:
- 1. table with concentrations of oxides in wt. % and elements in ppm or ppb
- 2. variation diagrams with two variables in cartesian diagrams, or three variables in triangular diagrams
- 3. normalization diagram used mainly for trace elements.
Modal composition
Volume proportion of selected rock-forming minerals expressed as vol. % is called the modal composition of rock. Depending on the desired precision, modal composition can be measured using several methods:
- 1. Visual comparison with schematic drawings (Fig. 3). This method can be applied to hand specimens and thin sections, but precision is low.
- 2. Use of an electromechanic counter with a regular pattern of points superimposed on a thin section. Each point is affiliated to a certain mineral and volume proportions of the counted minerals are then recalculated. The method is much more precise than the previous one, but it is also very time-consuming and tedious.
- 3. Usage of digital images taken either in transmitted polarized light or in back-scattered electrons processed using a computer program for image analysis. The measured mineral phases must be clearly distinguished using artificial colours.
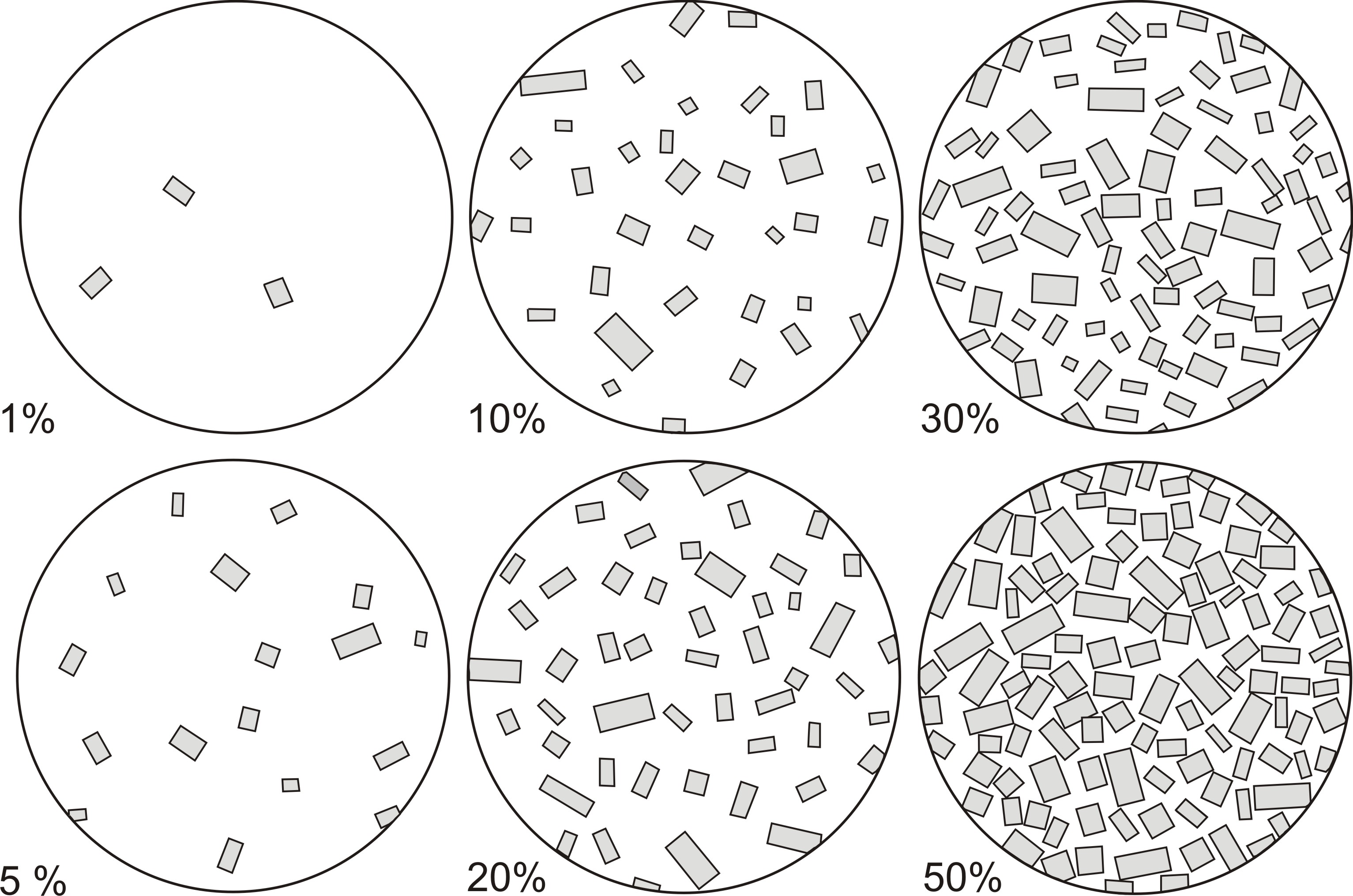
Fig. 3. Proportional composition of minerals in rock used for determination of modal composition (modified after Dudek et al., 1962).
Normative composition
Normative composition of a rock is hypothetical composition represented by normative minerals. Summary of the normative minerals with their abbreviations and chemical compositions is given in Table 2. The normative minerals are designed by italics in order to distinguish them from ordinary minerals (e.g. ab – albite). Many normative minerals are end-members of more complex solid solutions, representing true minerals occurring in nature (e.g. natural diopside is composed of enstatite – en, ferrosilite – fs, and wollastonite – wo, endmembers). The normative composition of a rock complements its bulk characteristics, which is included neither in chemical nor in modal composition. Normative composition is employed as an additional criterion of rock classification and for creation of phase diagrams in petrology.
The CIPW norm is recently the most frequently used method to characterize a rock by modal composition. The CIPW norm (acronym composed of initial lettters of author´s names) was introduced at the beginning of 20th century by W. Cross, J.P. Iddings, L.V. Pirson and H.S. Washington. The CIPW norm is calculated from bulk chemical analysis according to established rules described below. CIPW norms are calculated for each rock-type included in this Atlas of Rocks. The CIPW norm reveals a plethora of minerals, which would potentially crystallize on cooling of parental magma of a given composition. These minerals, however, could not be really present in the investigated rock, particularly if the rock still contains silicate glass. The CIPW norm also reveals, whether the rock is under- or oversaturated by silica. The SiO2-saturation belongs to the most important parameters of magmatic rocks. Quartz crystallizes from SiO2-saturated magmas and should be present also in the assemblage of rock-forming minerals. In contrast, SiO2-undersaturated phases, such as foids or olivine, crystallize from the magmatic rocks devoid of normative quartz. Normative plagioclase and feldspar followed by pyroxenes are calculated first, and finally quartz in excess of SiO2. If SiO2 is exhausted during the calculation, its deficit must be compensated by a normative mineral with a lower SiO2 content, but similar proportion of the remaining oxides. For instance, lack of SiO2 needed to create normative pyroxene can be compensated by affiliation of the equivalent amount of FeO and MgO to olivine, which contains less SiO2 than pyroxenes: molar ratio of (Mg,Fe)O to SiO2 in orthopyroxene (hy – hypersthene) equals to 1:2, whereas the same ratio in olivine represented by normative forsterite – fo and fayalite – fa, is 2:1 (Table 2). If there still exists a SiO2-deficiency in the norm, a portion of SiO2 and remaining oxides must be transposed from albite to nepheline, because the SiO2/Na2O molar ratios in albite and nepheline correspond to 6:1 and 2:1, respectively. Hence, 1 mole of nepheline created from 1 mole of albite liberates more SiO2 than conversion of 1 mole orthopyroxene to 1 mole of olivine. Hence, a higher SiO2 deficit in the rock results in the presence of normative nepheline. Nepheline and olivine are Si-deficient analogs of albite and orthopyroxene, respectively. Elimination of the Si-deficiency proceeds until the deficiency is removed and all other oxides are also exhausted. For instance, if normative nepheline does not eliminate the Si-deficiency, other Si-poor minerals are created: orthoclase is modified to leucite, wollastonite and diopside are transformed to dicalcium silicate – larnite together with olivine. Finally, in extremely Si-undersaturated rocks, leucite can be replaced by kaliophylite.
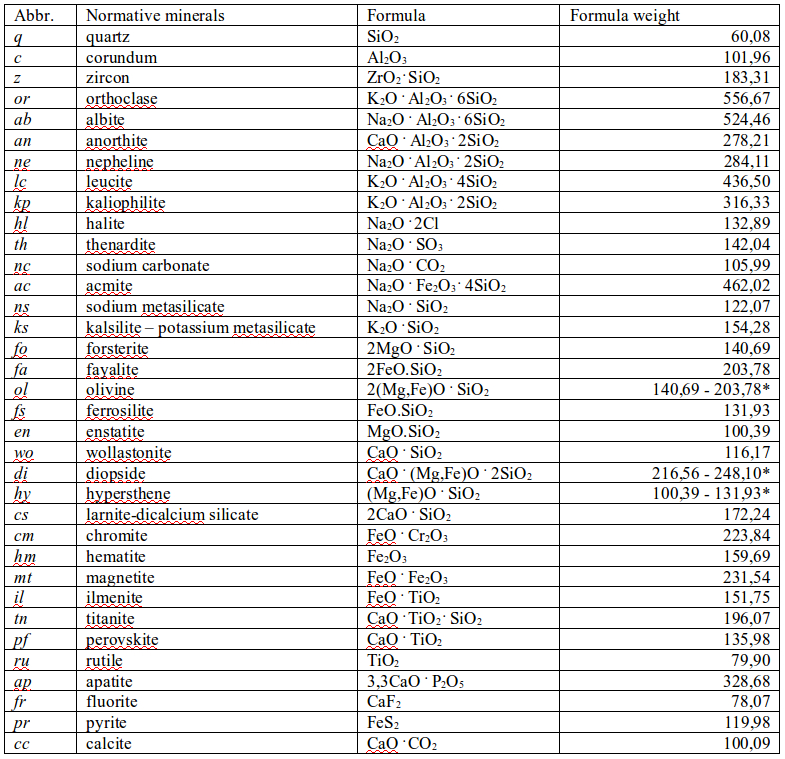
Table 2. Overview of standard normative minerals, their chemical composition and molecular weights (Winter, 2010).
The degree of SiO2-saturation is indicated by the following normative minerals:
- 1. Si-oversaturated rocks – normative quartz (q) and hypersthene (hy)
- 2. Si-saturated rocks – normative hypersthene (hy) or olivine (ol)
- 3. Si-undersaturated rocks – normative olivine (ol) and nepheline (ne).
Aluminium oxide Al2O3 is the second most abundant oxide in most magmatic rocks. Its saturation is an additional parameter used in classification of felsic rocks (Fig. 4).
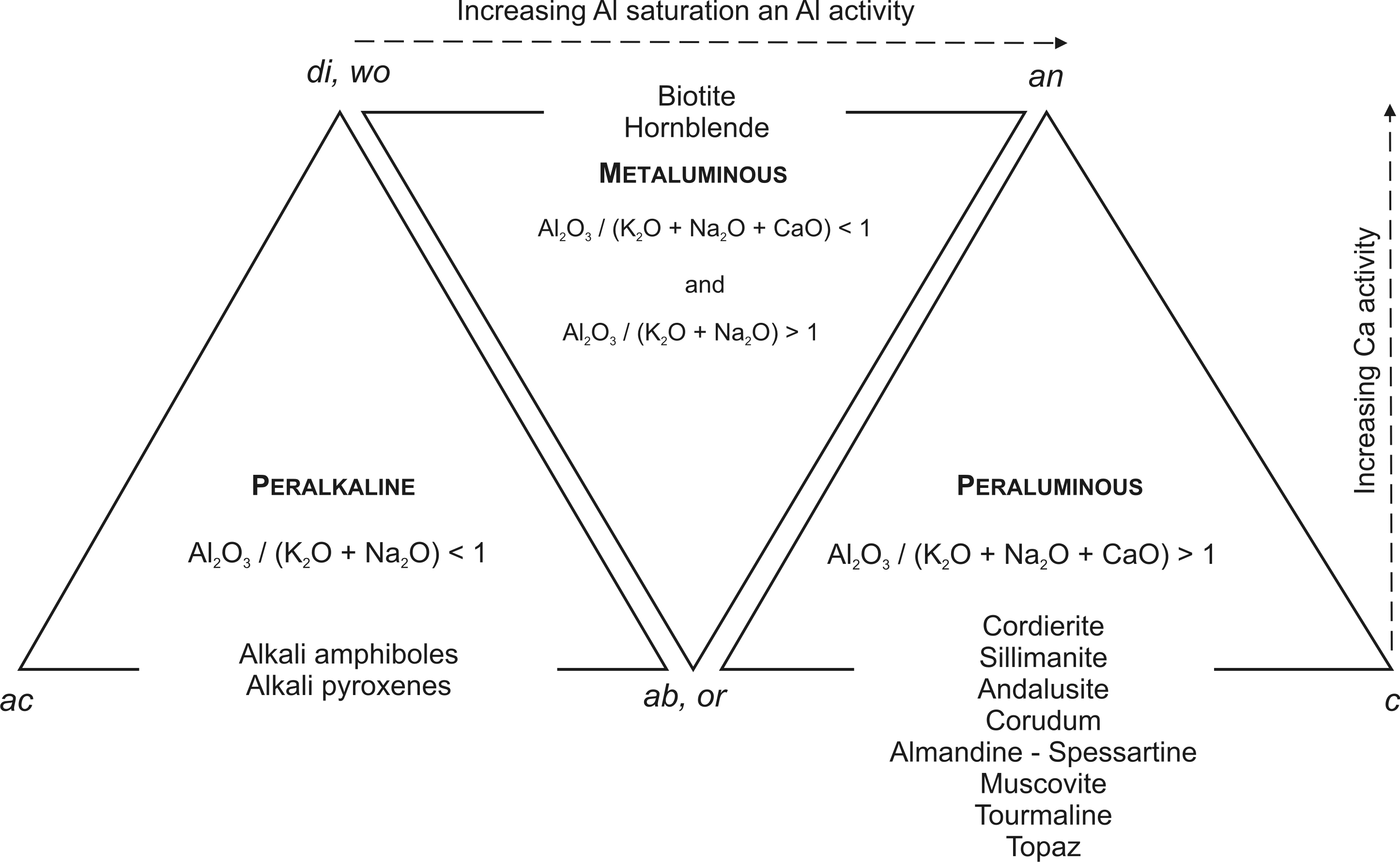
Fig. 4. Classification of felsic rocks based on the degree of Al2O3 saturation. Apices of the triangles are molecular ratios of normative minerals. True minerals present in natural rocks are listed within triangles (modified after Best and Christiansen 2001).
The Al2O3-saturation index is defined as the molecular ratio Al2O3/(K2O+Na2O+CaO), which equals to unity in feldspars, plagioclases and foids. In magmas, where foids or feldspars crystallize, each Al2O3 excess or deficit is compensated by crystallization of mafic and accessory minerals. Al2O3-oversaturated or peraluminous magmas crystallize micas, mainly muscovite, but also Al-rich biotite and Al-rich accessory minerals, such as cordierite, sillimanite-andalusite, corundum, tourmaline (needs also boron), topaz (needs also fluorine) and garnet of the almandine-spessartine series. Tourmaline, topaz and garnets can crystallize also from Al-undersaturated magmas. All peraluminous rocks are diagnostic of the presence of normative corundum (cor) in the CIPW norm. Al2O3-undersaturated, metaluminous magmas crystallize hornblend, Al-depleted biotite and titanite (its stability depends on the oxidation state of parental magma). Metaluminous rocks contain normative anorthite – an and diopside – di (or wollastonite – wo). The Al2O3/(K2O+Na2O) ratio in the metaluminous rocks is higher than unity, contrasting with the peralkalic rocks having this ratio lower than unity. Al2O3-deficient peralkalic magmas enriched in Na2O and K2O crystallize aegirine, riebeckite and aenigmatite, but they have normative acmite – ac and/or sodium metasilicate – ns, in their CIPW norm. In turn, they never contain normative anorthite – an.
Calculation of normative rock composition
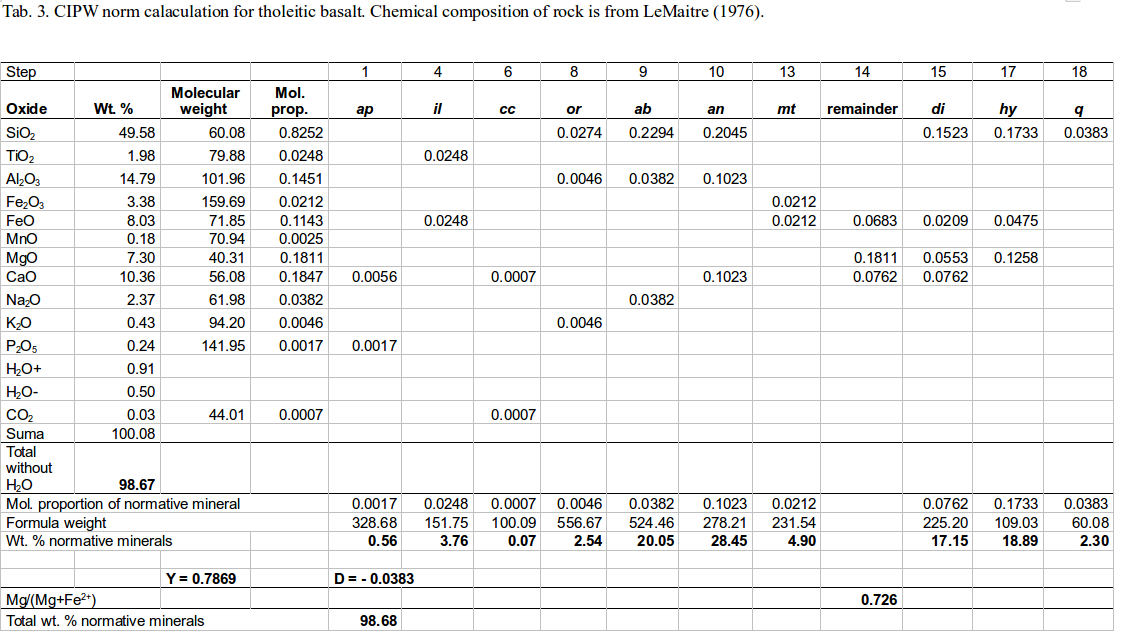
First step in calculating the CIPW norm is dividing the relative weight of each oxide by its molecular weight to obtain molecular proportion of the oxide. Minor concentrations of Ni and Mn substitute for Fe in common ferromagnesian minerals, and thus the molar proportions of NiO and MnO are added to that of FeO. Similarly, molar proportions of BaO and SrO are added to CaO. The calculated molar proportions of oxides are then distributed among normative minerals with ideal composition. The normative minerals can be viewed as the minerals that could potentially crystallize if the rock were cooled under perfect equilibrium conditions with the absence of water. The CIPW norm calculation can be done using simple mathematical functions included in an EXCEL spreadsheet (Table 3). This table contains sample calculation for a silica-oversaturated rock – quartz tholeiite.
First column in Table 3 contains bulk chemical analysis of the rock expressed in wt. %. Molecular weights of oxides are in the second column. The third column displays molar proportions of oxides. Allocation of molecular proportions of oxides preceeds until all oxides are exhausted and distributed among corresponding normative minerals. The molar proportions of normative minerals are then multiplied by molecular weights of the normative minerals to obtain their relative weight percentages – the CIPW norm. Sum of the relative weight percents of the normative minerals must equal that of oxides in the chemical analysis (without H2O). This is a check of validity of our calculation. The relative weights of normative minerals should be normalized to 100 %, if this had not been done for the chemical analysis prior to calculation of the CIPW norm.
Procedure for the calculation of molar proportions of normative minerals (modified after Phillpots and Ague 2009) consists of the following steps, in which the name of oxide refers to its molar proportion (column 3 in Table 3):
- 1. Allocate P2O5 to apatite – ap. Multiply P2O5 times 3.33 and subtract this number from CaO. P2O5 represents 2/3 of an apatite molecule, so multiply P2O5 times 2/3, and put this number in ap. P2O5 is now zero. The rest of CaO will be used in the calculation of other normative minerals. In contrast, phosphorus occurs only in normative apatite (5CaO + 1.5P2O5 + 0.5H2O = Ca5(PO4)3OH, where 1 mole of P2O5 is bound with 3.33 moles of CaO (5/1.5) to form apatite with the idealized normative formula Ca3.33(PO4)2. The apatite-bound water must be neglected because all normative minerals are anhydrous.
- 2. Allocate sulfur to pyrite – py and subtract 0.5S from FeO.
- 3. Allocate Cr2O3 to chromite – cm and subtract the equivalent from FeO.
- 4. Allocate TiO2 to ilmenite – il and subtract the equivalent from FeO. If TiO2>FeO, allocate excess TiO2 to provisional titanite – tn’, and subtract the equivalent of tn’ from CaO and SiO2. However, this step is done only if there is a CaO excess after creatiion of anorthite – an (step 10). Hence, the content of normative tn will be equivalent to the amount of available CaO. If there is still a TiO2 excess, this will be allocated to normative rutile – ru.
- 5. Allocate all F to fluorite – fl and subtract 0.5F from CaO.
- 6. Allocate CO2 to calcite – cc and subtract the equivalent from CaO.
- 7. Allocate ZrO2 to zircon – z and subtract the equivalent from SiO2.
- 8. Allocate K2O to provisional orthoclase – or’. Subtract the equivalent from Al2O3 and 6K2O from SiO2. If there is K2O excess (rarely), this is allocated to K-metasilicate – ks and the equivalent amount is subtracted from SiO2.
- 9. Combine the excess Al2O3 with the equivalent amount of Na2O and create provisional albite – ab’. Subtract 6Na2O from SiO2. If there is an Al2O3 deficit, go to step 11.
- 10. Combine the excess of Al2O3 from step 9 with the equivalent amount of CaO and create provisional anorthite – an’. Subtract 2Al2O3 from SiO2. If Al2O3>CaO, allocate the Al2O3 excess to corundum – c.
- 11. If there is an excess of Na2O over Al2O3 from step 9, allocate the equivalent amount of Fe2O3 to acmite – ac and subtract 4Fe2O3 from SiO2.
- 12. If there is Na2O excess in step 11 (extremely rarely), allocate it to sodium metasilicate – ns and subtract the equivalent from SiO2.
- 13. Allocate all remaining Fe2O3 to magnetite – mt and subtract the equivalent from FeO. If Fe2O3>FeO, allocate the excess Fe2O3 to normative hematite – hm.
- 14. All remaining FeO and MgO will be used to create pyroxenes (hypersthene and diopside) and olivine. Calculate ratio Mg/(Mg+Fe2+) ratio needed for creation of these normative minerals.
- 15. Allocate excess CaO from step 10 to provisional diopside – di’ .Calculate MgO/(MgO+FeO) ratio. The amount of MgO in di’ is equal to MgO/(MgO+FeO) CaO, and FeO in di’ is equal to CaO – MgO. In other words, CaO in di’ is equal to MgO + FeO in di’. Subtract 2CaO from SiO2.
- 16. If CaO > (MgO+FeO) allocate the CaO excess to provisional wollastonite – wo’ and subtract the equivalent from SiO2.
- 17. If CaO < (MgO+FeO) allocate the MgO+FeO excess to provisional hypersthene – hy’ and subtract the equivalent from SiO2.
- 18. Calculate the amount SiO2 allocated till now to normative minerals (the Y value). Calculate SiO2 deficit D = Y – total molar proportion of SiO2 in the column 3. If D<0 allocate excess SiO2 to normative quartz – q. This rock is SiO2-oversaturated and the CIPW norm calculation ends in this point.
- 19. If D > 0, the rock does not contain sufficient SiO2 for saturation of normative minerals created so far. Hence, some of them must be changed to other, containing a lesser amount of SiO2. Creation of new, less Si-saturated minerals must be done in a fixed order: provisional hypersthene is converted to olivine, provisional titanite to perovskite, provisional albite to nepheline, provisional orthoclase to leucite, provisional wollastonite and diopside to dicalcium silicate and olivine and finally, provisional leucite to kaliophylite.
- 20. If D < hy’/2, then ol = D and hy = hy’–2D. If D> hy’/2, all provisional hypersthene corresponds to olivine (ol = hy’/2) and a new SiO2 deficit is calculated as D1 = D - hy’/2.
- 21. If D1 < tn’, pf = D1 and tn = tn’ – D1. If D1 > tn’ all provisional titanite is allocated to perovskite and new SiO2 deficit is calculated as D2 = D1 – tn’. If no provisional titanite was created in step 4, set D2 = D1.
- 22. If D2<4ab’, convert a portion of the provisional albite to nepheline: ne = D2/4 and ab = ab’– D2/4. If D2>4ab’, all provisional albite is converted to nepheline (ne = ab’) and a new SiO2 deficit is calculated as D3 = D2 – 4ab’.
- 23. If D3 < 2or’, a portion of provisional orthoclase is allocated to leucite: lc = D3/2 and or = or’ – D3/2. If D3 > 2or’, all provisional orthoclase is converted to provisional leucite (lc’ = or’) and a new SiO2 deficit is calculated as D4 = D3 – 2or’. If no provisional wollastonite is available, D4 = D5 and proceed with the step 25.
- 24. If D4 < wo’/2 (in provisional wollastonite, but not in provisional diopside), allocate a portion of wo’ to dicalcium silicate (larnite) – cs: cs = D4 and wo = wo’ – D4. If D4 > wo’/2, allocate all provisional wo’ to larnite: cs = wo’/2. Calculate a new SiO2 deficit D5 = D4 – wo’/2.
- 25. If D5 < di’, a portion of provisional diopside is converted to larnite and olivine: cs = D5/2, ol = D5/2 and di = di’ – D5. Add new ol and di to those created in steps 20 and 24. If D5 > di’, change all provisional diopside to dicalcium silicate and olivine: cs = di’/2 and ol = di’/2 + ol’. Molar proportion of MgO in ol is a sum of those in di’ and ol’. Molar proportion of FeO in ol is calculated in the same way. Calculate a new SiO2 deficit D6 = D5 – di’.
- 26. If SiO2 is still in deficit, change a portion of provisional leucite to kaliophylite: kp = D6/2 and lc = lc’ – D6/2. In this step, the SiO2 deficit should be definitely eliminated.
If SiO2 deficit is eliminated in some of the steps 20-26, the calculation of molar proportions of normative minerals ends. The last step is then the multiplying of the molecular proportions of normative minerals by molecular weights to get relative weights of all created minerals (printed in bold in Table 3). Note that molecular weights of Mg-Fe minerals (diopside, hypersthene, olivine) depends on their Mg/(Mg+Fe) ratio. For instance, molecular weight of normative diopside is calculated as:
f.w. of di = XMg (f.w. of Mg-Di) + XFe (f.w. of Fe-Di)
Where f.w. is formula weight, XMg is Mg/(Mg+Fe2+) ratio and XFe is Fe2+/(Mg+Fe2+) ratio calculated from molar proportions of MgO and FeO prior to creation of normative diopside (Table 3). Formula weights f.w.of diopside endmembers are given in Table 2. Molecular weights of other Fe-Mg minerals (hypersthene, olivine) are calculated in a similar way. The recalculation involves all end-members; therefore molar proportion of a normative mineral can be simply multiplied by the corresponding molecular weight derived from its chemical composition.
Waste majority of CIPW norm calculations ends with the step 22 by creation of normative nepheline. Only very rarely other Si-unsaturated normative minerals are to be calculated. Calculation of CIPW norm for Si-oversaturated and Si-saturated rocks terminates with the creation of normative quartz in the step 18. Other less common normative minerals, such as halite – hl (from Cl), thenardite – th (from SO3) and fluorite – fl (from F) can be also calculated to eliminate these elements in chemical analysis (Winter, 2010).
References:
Best, M.G. & Christiansen, E.H., 2001: Igneous Petrology. Blackwell Science, 458 pp.
Dudek, A., Fediuk, F. & Palivcová, M. (1962): Petrografické tabulky. Příručka petrografické mikroskopie s atlasem struktur a textur. Nakladatelství Československé akademie věd, Praha, 304 pp.
Le Maitre, R.W. (1976): The chemical variability of some common igneous rocks. Journal of Petrology 17, 4, 589-598.
Philpotts, A.R. & Ague, J.J. (2009): Principles of igneous and metamorphic petrology. Second edition, Cambridge University Press, 667 pp.
Winter, J.D. (2010): Principles of igneous and metamorphic petrology. Second edition, Prentice Hall, 702 pp.